Il termine p-Tree è usato da Wolberg (vedi Appendice e-mail e Bibliografia) per definire una speciale struttura di dati particolarmente utile per modellare efficientemente spazi p-dimensionali con la kernel regression. La struttura è basata su un albero completamente binario con un’altezza prestabilita dall’analista col parametro H (TREEHEIGHT), in altre parole è un albero con esattamente 2H celle “foglie”. Ciascun punto di learning cade in una di queste leaf cells e lo spazio p-dimensionale è partizionato in maniera tale che il numero di punti per cella sia all’incirca costante: se nlrn è un multiplo di 2H il numero di punti di learning per cella è esattamente costante. In definitiva il p-Tree serve per raggruppare rapidamente i punti di learning più simili in celle per stimare ciascun punto di testing.
Se si specifica il numero di nearest neighbors da considerare (parametro numnn), allora ogni punto di y del test set sarà stimato in base a numnn learning points; ma per la stima di y non è necessario identificare esattamente i numnn punti più vicini: la scelta dei learning points ha una certa influenza sull’accuratezza della predizione, ma se la selezione dei punti più vicini è ragionevolmente approssimata, allora, nella maggior parte dei problemi reali, il calo di bontà delle previsioni è contenuta.
Si può scegliere come nearest neighbors solamente i punti contenuti in una leaf cell, oppure creare una matrice di adiacenza per identificare tutte le celle adiacenti ad ogni cella, in modo che l’algoritmo possa individuare non solo i punti della cella in cui risiede il punto di test da stimare, ma anche quelli di tutte le celle adiacenti. Così facendo aumenterà la probabilità di trovare tutti i punti di learning più vicini a quel punto di test, soprattutto quando si trattano serie con una grande componente di “rumore”.
Purtroppo, però, più la dimensionalità del problema cresce, più le celle adiacenti aumentano esponenzialmente e cercare i punti vicini diventa abbastanza costoso. D’altro canto, trascurando alcuni nearest neighbors, si ha una minima perdita in termini di accuratezza predittiva: si può ottenere, infatti, una eccellente capacità previsionale anche usando solo i punti nella cella di un dato test point (Fast Kernel Regression, vedi cap. 4.3).
Tuttavia, tra la ricerca dei nearest neighbors effettuata in una sola cella e la ricerca in una cella ed in tutte quelle adiacenti alla stessa, esiste una via intermedia di procedere. Viene introdotto un nuovo parametro chiamato numcells, che stabilisce il numero massimo di celle adiacenti da considerare nella ricerca dei nearest neighbors. Chiaramente il tempo computazionale cresce al crescere di numcells, ma solo fino al valore limite pari al numero massimo di celle adiacenti esistenti, infatti, se fosse specificato un valore di numcells superiore al numero totale di celle, l’algoritmo esaminerebbe solo la cella che ospita il test point e tutte le celle adiacenti esistenti.
L’introduzione del parametro numcells generalizza il concetto di p-Tree in quanto consente all’operatore di stabilire quale metodo di ricerca dei nearest neighbors scegliere. Se numcells=1 si avrà il caso più semplice in cui l’algoritmo di ricerca dei nearest neighbors opererà solo in una cella, se numcells è pari al numero totale di celle adiacenti, l’algoritmo ricerca nella cella del punto di test e in tutte le altre adiacenti, infine, se: 1 < numcells < “numero totale di celle adiacenti” si ha un algoritmo di ricerca intermedio tra i due citati.
Ricapitolando, il p-Tree è un semplice modo per creare l’equivalente della bandwidth in p dimensioni. Una volta che l’albero viene costruito, la cella in cui risiede il punto di test da stimare viene localizzata in un tempo linearmente proporzionale con l’altezza H dell’albero (O(H)) e la struttura dei dati dovrebbe consentire un immediato accesso a tutti i learning points
della cella. Se numcells >1 le celle adiacenti verranno velocemente identificate tramite la matrice di adiacenza e successivamente saranno accessibili i punti di learning.
L’uso del p-Tree è basato, dunque, sulle seguenti procedure:
− costruzione del p-Tree di altezza H utilizzando i nlrn punti di learning che verranno partizionati in 2H celle;
− se numcells >1, creazione della matrice di adiacenza;
− per ogni punto del test set:
− localizzazione della cella del p-Tree che contiene il test point;
− se numcells >1 , ricerca delle numcells–1 celle adiacenti;
− utilizzazione delle numcells celle per cercare i numnn punti di learning più vicini;
− impiego dei numnn punti di learning trovati per predire y in ogni punto del test set;
− ricorso ai valori stimati di y per determinare un criterio di modellamento appropriato. Alcune osservazioni sulla complessità del p-Tree di altezza H in uno spazio p-dimensionale usando nlrn learning points possono essere le seguenti:
− il massimo numero di classificazioni richieste per procedere dal livello
–1 al livello i sono 2(i – 1) ;
− per ogni livello i ≤ P dovrebbe essere scelta una differente dimensione per la nuova classificazione, in particolare, si dovrebbe scegliere la dimensione con range maggiore;
− se H > p, per ogni classificazione ai livelli i > p, si dovrebbe ordinare in base alla dimensione più lunga;
− gli ordinamenti da fare fino al livello H sono approssimativamente
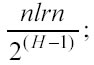
Il tempo massimo necessario per tutte le classificazioni può essere stimato considerando il tempo per ordinare n elementi in una lista: O(n*log2(n)). Si può così sviluppare un’espressione generale che indichi il tempo massimo per tutti gli ordinamenti fino al livello H:
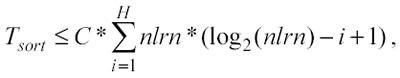dove C è una costante che dipende dalla potenza del computer.
L’espressione è una disuguaglianza perché non tutti gli ordinamenti devono
necessariamente essere attuati.
La sommatoria si può sviluppare e la disequazione precedente si trasforma
nella seguente:
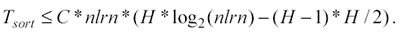
Questa espressione evidenzia che il limite massimo di tempo richiesto per effettuare tutte le classificazione di tutti i livelli è inferiore ad H volte il tempo necessario ad un unico ordinamento di tutti gli nlrn elementi. Inoltre, il tempo reale potrebbe essere significativamente inferiore a questo limite massimo nel caso certi ordinamenti in alcuni livelli risultassero non essere necessari: un nuova classificazione è necessaria, infatti, solo se l’ordinamento è basato su una dimensione differente rispetto alla dimensione scelta nel livello precedente.
Successivo: 3.3 L'utilizzo del P-TREE
Sommario: Index